Solution Of Triangles - 1

Every triangle has 3 angles and 3 sides. Given any 3 quantities out of 3 angles and 3 sides (at least one of which is a side) are given then remaining 3 can be found , which is termed as solution of the triangle. Many interesting relation among these quantities will be discussed in this section. Which formula is to be used where is a very important point here, as a use of wrong formula might lead to large calculations. So be prepared to see some very interesting stuff.

Terminology

Side AB , BC, CA of a DABC are denoted by c, a, b respectively and is semi perimeter of the triangle and D denotes area of the triangle.

Since Rule:

How?

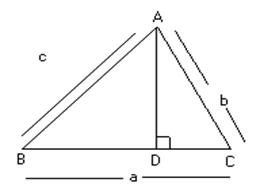
                        Fig (1)

Draw AD perpendicular to opposite side meeting it in point D.

In DABD,

Þ AD = cSinB

In D ACD,

Þ AD = bSinC

Equating 2 values of AD we get

cSinB = bSinc

Similarly drawing a perpendicular line from B upon CA we have

Illustration 1:

Given that ÐB=30, C=10 and b=5 find the angles of A and C of triangle.

Ans:

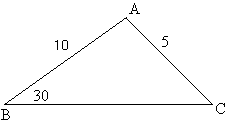
Fig (3)

By using sine rule,

Cosine Rule:

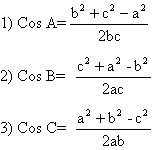
How?

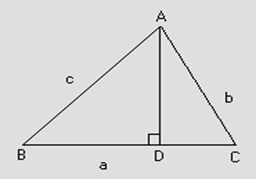
                                                           Fig (4)

Let ABC be a triangle and let perpendicular from A on BC meet it in point D

Now      AB²= AD²+BD²

                     = (BC-CD) ²+ (AC²-DC²)

                     = BC²+CD²-2BC.CD+AC²-DC²

                     = AC²+BC²-2BC.CD                                                     ------------------ (1)

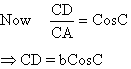
So, equation (1) is now

c² = b²+a²-2abCosC

Similarly CosA, CosB can be found.