The Concepts of Chemical Equilibrium for IIT-JEE

Concepts Of Chemical Equilibrium

History of chemical eqm started from At beginning of 18th century whole idea of chemical eqm. is based on there basic ideas: in complete reaction, reversibility & dynamic. Berthollet, Clande Laus (1748-1822) was pioneer in this field. He tonght chemistry to Napolean & ment to Egypt in 1798. He observed these that high conc. of sod. Carbonate by Lake Neutron on edge of the desert. He conclanded that under prevailing condition, Nice in upper layee of soil hard reacted with calcium carbonate from nearby lime stone hills. From there he started on working of chemical eqm. Chemical Equilibrium gives us the answer that why we cannot have 100% yield in a reaction? This chapter is of prime importance in physical chemistry. If opposing processes involve chemical changes. Chemical Here eqn. is called chemical eqm.

aA + bB xX + yY

Physical Eqn.:-

1. Solid – liquid Eqn. :- (Meeting office)

Rate of melting of ice = Rate of freezing of water

H₂O(s)H₂O(l)

Temp. at which solid & liquid form of pure substance are in eqm. atm. Pressure c/d freezing point.

2. Liquid – Gas eqm.
(Evaporation of water in closed vessel):

Rate of evaporation= Rate of condensation

H₂O(l)H₂O(g)

3. Solid – Solution eqm.
:- Dissolution of sugar in water

Rate of dissolution=Rate of precipitation

Sugar (Solid)Sugar(insolution)

Solubility :-
Amt. Of solid in gms. That dissolves in 100g of solvent to from saturated solution at particular temp.

4. Gas - solution eqm. -
(Dissolution of gas in liquid)

Co₂Co₂(in solution)

Reversible Rxn. :-
Rxn. which takes place not only in forward direction but also in backward direction. Under same condition

A + BC + D

PCL_S(g)PCL₃(g) + CL₂(g)

direction

eq. AgNo₃(aq.)+NaCl(aq.) AgCl(s)+NaNo₃(aq.)

Concept of chemical Eqn. :

A + BC + D

At eqm.

Rate of farward rxn. = Rate of backward rxn.

C_aCO₃(S)C_aO(s) + CO₂(g)

Characteristics of chemical Eqm.:

1. At eqm. , conc. of each of reactants & products becomes constant.

2. At eqm. , rate of forward rxn. , becomes equal to rate of backward rxn. So, eqm. is dynamic in nature.

3. A chemical eqm. can be established only if none of products is allowed to escape out or separate out as a solid.

eq. AgNo₃+K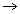ClAgCl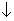+ KNo₃

4. Chemical eq. Can be attained from either direction

eq. N₂O₄(g)2NO₂(g)

(Colourless)   (Raddish brown)

5. Catalyst does not alter state of eqm.

Question: why catalyst does not alter state of eqm.

Answer: Catalyst speed of forward as well as back was reaction to same extent. So, eqm. is not disturbed.

Law of Mass Action:-
Rate of rxn. is proper to product of active masses of reactants, each raised to power equal to its stoichiometric coiff. as in balanced equation

Law of Chemical Eqn.:-

A + BC + D

Applying Law of mass action.

Rate of forward r*nk=

Rate of backward rxn. a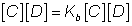

At eqm.

Rate of forward rxn. = Rate of backward rxn.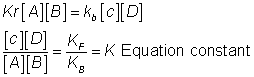

aA + bBxX + yY

By law of Mass action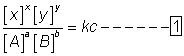

for gas Phase reaction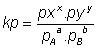

Relation b/w kp & kc

aA + bBxX + yY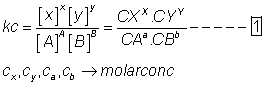

if x,y, A &B are gaseous, then

If gases are ideal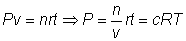

Q.why?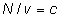

ans:- n/v =no. of moles/litre=c for gases A,B,X & Y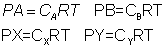

Putting these values in eq (ii)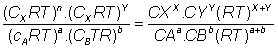

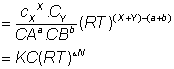
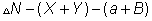
= no. of moles of reactants.

Illustration
:- At 773k, eqn constant kc for r*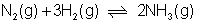

is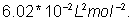

.

Calculate value of Kp at same temp.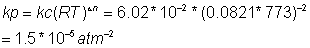

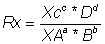
where x_c, x_D,x_a& x_b
are margin

partial pressure= Molefraction xTotal pressure (p_T)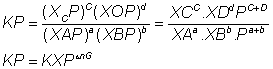

NOTe: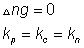

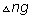
=no. of moles of product(gas)-no. of moles of reactant(gas)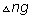

Take molar conc. & pressure of solids as units.

Characteristics of Eqm. Constant:
(1) Value of eqm. constant for given rxn. is always constant depending only upon temp. of rxn. is independent of conc. of reactants with which me start or direction from which eqm. is approached.

(2) If rxn. is reversed, value of eqm. constant is reversed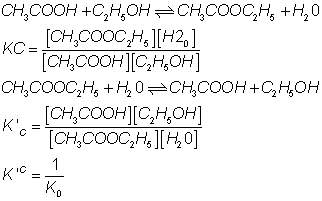

for new eq. Is square root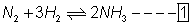

then for rxn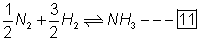

value of eqn. constant k'=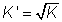

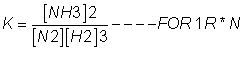
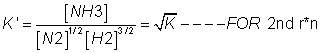
4. if eq.(having eqn constant k) is written in two steps (having eqn constant k1 &k2) then k1xk2=k

N₂+ 2O₂ 2NO₂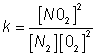

N₂+ O₂ 2NO

2NO + O₂2NO₂

for 1st step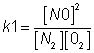

for 2nd step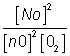

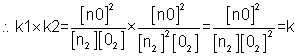
(V) Value of eqm. constant is not affected by catalys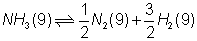

for reverse reaction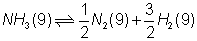

dividing by two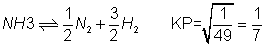

Thermodynamics of chemical equilibrium

for a process at constant T and p if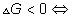

process is spontaneous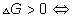

process s spontaneous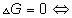

process is equilibrium

Dumb quesstion: what is g?

sol:- g is gibbs free energy and is defined as G=h-ts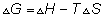

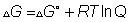
where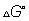

is the value of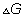

at standard condition Q= reaction quotent

Q: what is reaction quotient?

sol:- For areaction aA + bBxX + yY

at any time r.Q =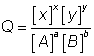

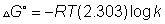
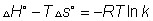
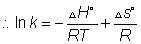
Differenteat both sides wrt T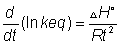

Nant haff's equation

at two different temperature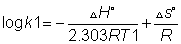

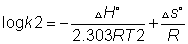
So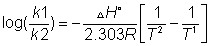

For reverse rxn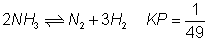

on dividing by 2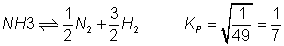

eq. H₂(g) + I₂(g)2HI(g)

Fe³⁺(aq.) + SCN(aq.)[Fe(SCN)]^2T(aq.)

Heterogeneons Eqn.:-
When reactants & products arepresent in two or more than two phasees.

eq. CaCo₃(s)CaO(s) + Co₂(g)

Writing Expression for Eqn. Constant(k):-

[ Pure solid ] = 1 & [ Pure liquid ] = 1 (if present as solvent)

For Hetrogenous Eqn.:-

(i) H₂(g) + I₂(g)2HI(g)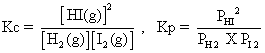

(ii) PCl_s(g)PCl₃(g) + Cl₂(g)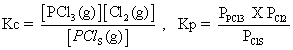

For Hetrogeneous Eqn.:-

CaCO₃(S)CaO(S) + CO₂(g)

By law of chemical eqn.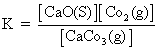

By conversion, Putting [ CaO(S)] = 1 & [CaCo
₃
(S)] = 1
K = [CO₂(g)]K_p= P_CO₂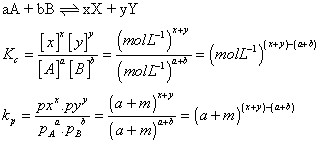

Application of equation constant

(1)
Predicting extent of r*n
:-

(a) larger value of eqn. constant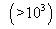

shows that forward

rxn is favoured.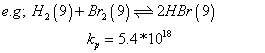

(b) intermediate value of k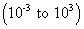

shows that conc. of reactants & products are comparable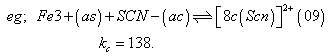

(c) low value of shos that backward rxn is favoured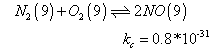

2.predicting direction of rxn:-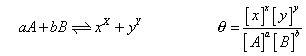

(1) If Q = k, rxn. is in equetion

(2) If Q > k, Q will tend to so as to becomes equal to 1.so, rxn. will proceed in backward direction.

(3) if Q < k, Q will tend to increase, So rxn. will proceed in forward direction.

Versal & when eqn. was dessociated into PCl₃& Cl₂. Calculate eqn. constants K_p& K_cfor this rxn.

Ans
PCl₅PCl₃+ Cl₂

% dissosiation of PCl₅at equation = 40%

Amount of PCl₅, PCl₃& Cl₂
at equation will be

PCl₅= 2-0.8 = 1.2 mole, PCl₃= 0.8mole & Cl₂= 0.8 mole.

Domb qouestion: [{Q. why mole of PCl₃& Cl₂are 0.8 ]

Ans. 1 mole of pcls on dissociation gives 1 mole of PCl₃& 1 mole of Cl₂ Vol. of container = 2L

molac conc. at equation will be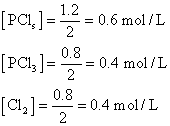

By law of chemical equation.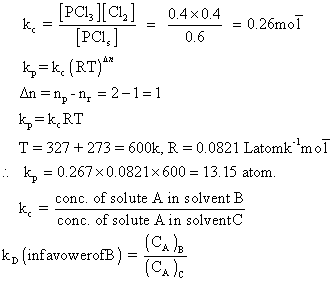

Illustration
:- Ratio solvelity of oxialic acid in H₂O and ether is 10. 1 L of eq. Sol. Of oxalicacid in H₂
O i0 g/L. was mixed with 100 ml of ether Calculate conc of oxalic acid in g/L in ether long.

Ans. Let x gm of oxalic acid present in either them(10 - x)g is present in H₂O.

Ko=10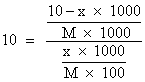

on solving x = 0.0999 g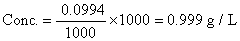

Deg. of dissociation in term of v.d
:-

Using the results of solutions chapters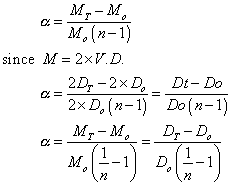

Illustrartion
: 0.0753 g of selenium vapours occupiedmol of 78ml at STP. Selenium is in state of equation.

Se₆(g)3Se₂(g)

Calculation deg. of dissociation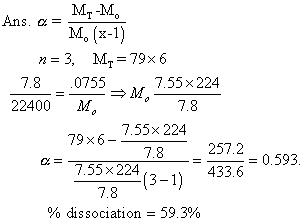

Factors affecting equation:-

(1) Chyange of conc. Of any reactant or product

(2) Change in temp. of system

(3) Change in pressure of system

(4) Tradition of catalyst

(5) Addition of inert gas.

Effect of addition of catalyst
:- Addition of catalyst does not disturb eqn. But helps in attainment of eqn. quickly.

(a)
If rxn takes place at constant vol.(closed vessel)
:- Addition of inert gas will not chang mole conc. Of reactants & products. So, state of eqn. Will remain unaffected.

(b) If rxn. Takes place at constant pressure, Hence dissociation of pcl3 increases.

Dumb quation:-[Q. How this happen?

Ans. Since p is cnstant, so addition of inert gas will Total volume. So, at equation, molec conc of each reactant old products will . So,kc is constant at constant temp.

So, to keep kc constant either [PCl₅]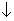should or [PCl₃] & [Cl₂] should. This happen only if PCl₅dissociates.

Le chathelier's principle:-
If a in eqn. Is subjected to a change of conc. Temp. of pressure, eqn. Shifts in direction that tends to undo the of the change imposes.

(1) Effect of conc.:-

A + BC + D

If rxn is in eqn. Mole of A or B is added, then ,according to Le chatelic's principle effect will be to
conc. Of A & B react to frome C & D. I,e;eq m. shifts in forward direction. Shift in forward.

(2) Effect of temp.:-

Every rxn. is made up of two opposing rxns. If to rewards rxn. Is exothermic, then backwardrxn.

If temp. is

,I,e; heat is supplied to system; according to the chateliec princple. i,e; eqn. Will shift to side heat absorbs heat I,e; in backward direction & vice versa.

Note
:- Exothermic rxn are forward by low temp. whereas end. thermic rxn. are favoured by high temp.

(3) Effect of pressure:-
Significant role to play only in case of gaseons rxn.

N₂O₄(g)2NO₂(g)

1 mole 2 mole

Forward rxn. Occurs with

in no. of moles & viseversa. If pressure on system

, then according to Le chateliec's principle , eqn. Will shift in direction in which pressure

or no of moles (b/c pressure is directly proportional to no. of moles). Since backward rxn. Takes place with in no of. moles. So,

in pressure will favovr. Combination of NO₂molecules to N₂O₄.

Note
:-

(1) Low pressure tavours those rxns which accompany by

in total no of moiles & vice versa.

(2) Pressure has no effect on eqn. Rxn which proceed which no change in total no. of moles. So,

in volume will shift eqn. In direction in which no of moles decreases.

I,e; eqn. Constant does not change with temp.

(ii)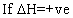
log(k₂/k₁)= +velog k₂>log k₁ 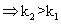I,e; eqn. Constant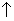with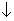in temp.

(iii)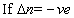log(k₂/k₁) = -velog k₂< log K₁ 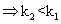I,e; eqn. Constantwithin temp.

Q.1 Calculate eqn. constant for rxn.

H₂(g) + CO₂(g)H₂
O(g) + CO(g) at 1539K, if eqn. constants at 1395K for following are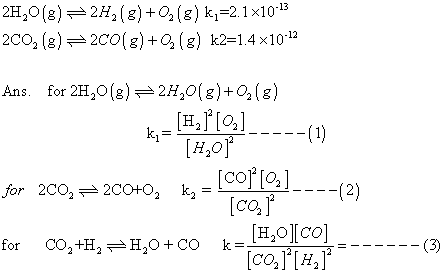

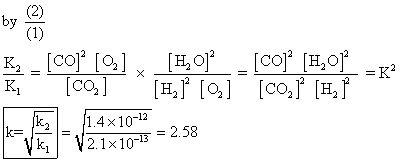
Q2.for reaction

A + B3C at 29⁰
C, 3L vessel contains 1,2,4 mole A, B & c resp. predict direction of rxn .

if (a)k_cfor rxn. is 10

(b) k_cfor rxn is 10.66

Ans.
:- A + B3C

Before rxn; [A] = 1/3

[B] = 2/3

[C]= 4/3

so,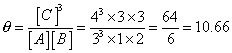

and this [c] must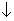

or [A] & [B] should so, rxn mole occurs in backward direction

(b) Q = K_c
, So, rxn. is in eqn.

Q.3 At temp, 2AB₂(g)2AB(g) + B₂(g)

with deg association 'x' which is small compared to unity. Device expression for 'x' in terms of eqns. Const. K_p& total pressure P.

Ans. 2AB₂(g)2AB(g) + B₂(g)

Mole after dissociation

Mole after dissociation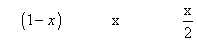

Total mole at eqn.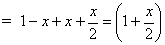

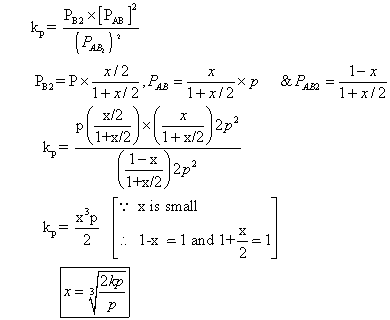
Q.4:- k_CFOR a₂(G) + b₂(g)2AB (g) at 100₀
C is 50. If one line flask containing 1 mole of A2 is connected with a 2L flask containing

2mole of B2 ; How many mole of AB will be formed at

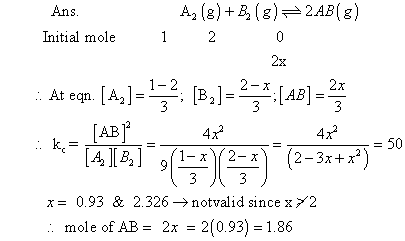
Q.5 N₂(g) + O₂(g)2NO(g)

was established with an eqn. constain K
_c= 2.1 X 10^{- 3}. At eqn. mole % of No. was 1.8. estimates initial composition of air in mole fraction of N₂& O₂.

Ans: N
₂
(g) + O₂ 2NO

initial a (100 - a) 0

final (a - x) (100 - a - x) 2n

given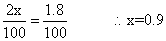

also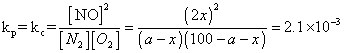

a = 79%, 100 - a = 21%

Q.6: k_pfor rxn. N₂+ 3H₂ 2NH₃is 1.6 X 10^-4atm^-2at 400⁰c what will be k_pat 500⁰
C ? Heat of rxn. in this temp. range is - 25.14 KCal.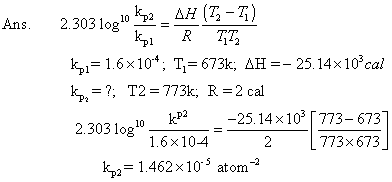

Out K_pfor rxn. Also report K_p&G⁰forN₂+ 3H₂ 2NH₃at 25⁰C

Ans. -
G⁰= 2.303 RT log₁₀K_p- ( - 16.5 X 10³) = 2.303 X 8.314 X 298 log₁₀K_p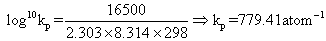

K_p¹for N₂+ 3H₂ 2NH₃K_p¹= (K_p)²= (779.41)²= 6.07 X 10⁵atm^{- 1}Also
G^0¹= 2.303 X 8.314 X 298 log₁₀(6.07 X 10⁵) J

=32.998 KJ

G^0¹= -32.998 KJ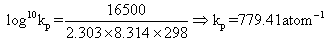

Q.9 At S4 Ok & 1 atom, N₂O₄is 66% dissociated into NO₂
what mol. of 10g N₂O₄occupy under these condition

Ans:-   N₂O₄2NO₂

initial 1             0

at eqn

total mole at eqn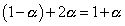

but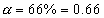

Total mole of eqn. = 1 + 0.66 = 1.66

1 mole of N₂O₄
is taken, mole at eqn.=1.66

mole of n2o4 is taken ,mole at eqn. =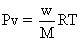

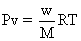
1 X v = 0.18X0.0821X340 = 5.02 L

Q.10 heat of rxn for rxn. At constant vol. is 1200 cal more than at constant pressure at 300k. calculate ratio of eqn. Constant k_p& k_c.

Ans.
E =H = 1200 Cal. Whrere
E is heat of rxn. at constant volume &
H is heat of rxn. at constant pressure

H =E +nRT

nRT = -1200

n = -1200 / 2X300 = -2

K_p= K_c(RT)ⁿ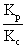= (0.0821 X 300)^-2= 1.648 X 10^-3

Q.1. 0.96g of HI sere heated to attom eqn. 2HIH₂+ I₂
rxn. mixture on titration required 15.7 ml of N/10 hypo sol. Calculate deg. of dissociation of HI.

Ans.         2HI H₂+ I₂

mole at t = 0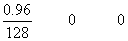

= 7.5 X 10
^-3

at eqn.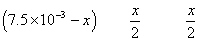

meg. Of I₂
formed at eqn. = meg.of hypo used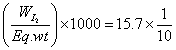

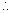Eqn. of I₂
=

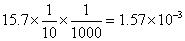
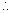
Mole of I
₂
formed =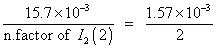

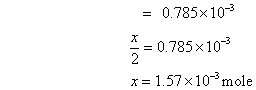
Deg. of dissociation of HI =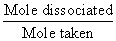

=

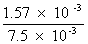
= 0.209 = 20.9 %

Q.2 An eqn. Mixture of

CO(g) + H₂O(g)CO₂(g) + H₂(g)

present in a vessel of 1 L capacity at 815c was found by analysis to contain 0.4 mole of Co, 0.3 mole of H₂O, 0.2 mole of Co₂and 0.6 mole of H₂
(a) Calculate kc

(b) Toconc. to 0.6 mole by adding co₂to vessel, how many mole must be added into eqn mix at mole at eqn 0.4 0.3 0.2 0.6

(b) Suppose 'a' mole of CO2 are forced in vessel at eqn.; by doing so rxn proceeds in backward direction

i.e                       Co₂+ H₂ CO + H₂O

at intial time (0.2 + a ) 0.6 0.4    0.3

at eqn. (0.2+a-0.2) (0.6-0.2) (0.4+0.2) (0.3+0.2)

a           0.4           0.6     0.5

Q.3 Deg of dissociation is 0.4 at 400k and 1 atom for gaseous rxt PCl
_s PCL₃+ CL₂
Assume ideal gas calculate density of eqn mixture at 400k and 1 atm.

(Atomic mass of p=31& cl=35.5)

Ans:   PCl
_s PCL₃+ CL₂

intial mole 1    0        0

At eqn. (1-0.4)   0.4   0.4

Total mole at eqn. = 1 - 0.4 + 0.4 + 0.4 = 1.4

Q.5 Heat enthalpy standard free energy change for

eqn.   Z_n(S) + H₂O(g)Z_nO(s) + H₂(g)

eqn Are 224 kJ mol
^-1
and 33kjmol respectively at temp 920 calculate temp at which eqn constant becomes greater than

(1) Assume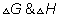

remains constant.

Ans.
G⁰= -2.303 RT logK

33000 = -2.303 X 8.314 X 920 log k

k_920k= 1.34 x 10^{- 2}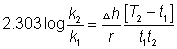

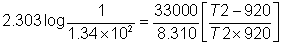
T₂= 1078.5 K.

SO, At any temp above this k will be greater than

Hard type

Q.1:- Solid nh4 on rapid healthy in aclosed vessel at 357 develop a constant pressure of 275 mmHg owing to partial decomposition of NH₄I into NH
₃& HI . calculate final pressure developed at eqn.k_pfor dissociation of HI is 0.015 at 357 C

Ans:- NH₄I(g)NH₃(g) + HI(g)-----(1)

for this eqn 2p=275 --> p=137.5

So k_pfor eq. (1)

K_p= P_NH3XP_HI= 137.5 X 137.5 ---------(2)

For     2HIH₂+ I₂
1        0    0

(1 - x)   x/2   x/2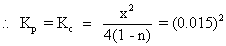

Dumb question
: why we have taken kp (0.015)²?

Ans: K
_pfor division of HI = 0.015

HI

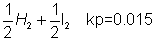
K
_p
= 0.015

2HIH₂+ I₂    K_p= (0.015)₂x = 0.2

Again since HI decomposes rxn proceeds in forward directioal (by Leehatetics Principal)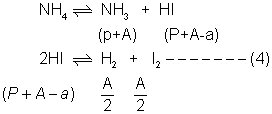

But a = (P + A) X 0.2

also k_p
for final eqn (3)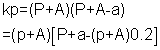

= 0.8(P + A)²But K_p
= 137.5 X 137.5

0.8(P + A)²
= 137.5 X 137.5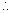

P + A = 153.73

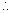A = 16.22

a = (p + A) X 0.2 = 153.73 X 0.2 = 30.75

Total pressure at eqn =PNH₃+PHI+PH₂+PI

=(P+A)+(P+A-a)+A/2+A/2

=2p+2A

=2(p+A)= 2x153.73

=307.46 mmHg

Q.2: when 1 - Pentyne (a)is treated with 4n atc. KOH at 175 it slowely get converted into an eqn mix of 1.3 % 1 pentyne 95.2% 2 pentyne(b) of 1,2 pentadiene (c)eqn. was maintained at 175c calculate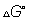

for following eqn.

from calculated value of g1 and g2 indicate order of (a) (b)(c) write a reasonable rxn mechanism in showing all intermediates reading to (A)(B)(C)

= 16.178 KJ

Stability order for A & B is B > A

Similerly for B
C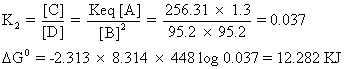

So, stability order for B and Cis B > C

Total stability order is B><>A

Q3. N₂& 0₂
combine at a giventemp to produce no. at eqn the yield of no is x% by volume. If x =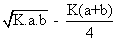

where k is is eqn constant given rxn. at given temp and a and b volume % of n2 &o2 respectively in intial pure mixture what should be the intial composition of reacting mixture in order that max. yield of nois ensured? also repo max value of k at which x is maximum?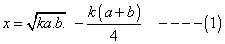

'x' is maximum only when condition of maximum are fulful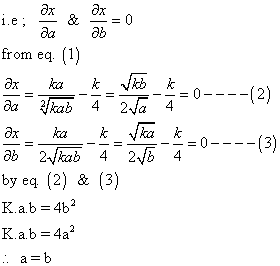

Note: this valid only when k<4 because if a = b Eq.(1)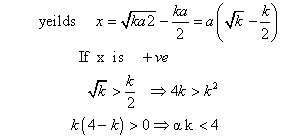

Equilibrium

Physical Eqn.

Low of mass action

Law of chemical Eqn.

Eqn.constant

Revessible rxn.

Forward rxn

Backward rxn

Gibbs free energy and Spontaneity

Homogeneous Equilibrium

Heterogeneous Equilibrium Le chatelier's principle

Source: goiit.com

Related Guides