trignometric-ratios-and-identities-1

The word trignometry is devided from 2 greek words
(1) Trigonon and

(2) Meetron

Trignon means triangle and metron means measure So, is science of measuning angle .A very interesting branch, it is used in almost all other branches of mathematic whether it be coordinatc goemetry or it be calculus.

For a given angle 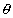in a right angle these ate six fossible ratios of 2 sides and hence there are 6 trignometric functions. These are extremely useful in simplefying many cliculations in mathematics. So lets stady these in more details.

Trignometric functions:
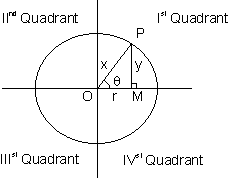
Let O be centre if circle of radius r . Let a may po form an angle 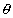at centre of circle. Drop a 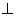pm.
So, in OPM we obserre.
sin 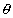= 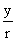, cos=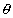



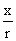
ton = ;
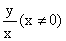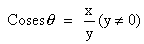
Further more about these 6 trignometric ratios is covered in this table.

Illustration 1.
Find the sol^r of the equation e^{ln cos x} = 2 ?
e^{ln cos x} = cos x ^lne = cos x
cos x = 2
Now the range of cos x is - 1 to 1 .
So, the equation has no solution .

Trignometric function of allied angles:
If 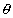is any angle then - 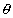, 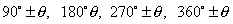etc are called allied angles of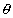

Remork: (1) If we have allied angle 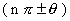where n is any integer then ratio remains the some and sign ( +ve and -ve) is given according to the quadrant in which 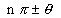lies
(assuming 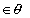I^st Quadrant).

(2) If we have allied angle 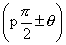where P is an odd integer then ratio changes i.e 'sine' changs to 'cosine' ; 'cosine' changes t 'sine'; tangent and 'cosecant' changes to 'secant'changes to 'cotangent', 'secant' changes t 'cosecant' and ' cosecant' changes to 'secant' The sign (+ve or -ve ) is given according t quadrant in which 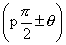lies(assumtg 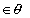I^stQuadrant.