trignometric-ratios-and-identities-2

Illustration 2:
Find the value of tan (1020⁰) ?
1020⁰ = 10 X 90⁰ + 30⁰
If lies in the IV ^th Quadrant.
So, tan (10 X 90⁰ + 30⁰ ) = - tan 30⁰
= -

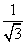
Trignometric Ratios of Compound angles:

(1) sin (A + B) = sin A cos B + cos A sin B
Why?
Draw < A o B = < A and < boc = < B .
And find any point P on oc.



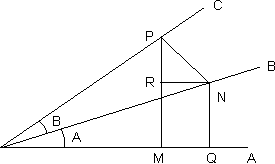
Draw PM and PN to OA and oB respectively.
Through N draw NR parrallel to AO t meet MP in R and other N OA
< R P N = 90⁰ - < P N R
= < R N O = < NO 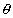= < A
So, sin (A + B) = sin A o P =
=
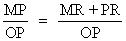
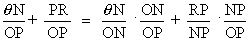
= sin A cos B + cos A sin B .

(2) os (A + B) = cos A cos B - sin A sin B
Why ?
cos(A + B) = sin( 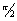- (A + B))
= sin(( 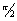- A) - (-B))
= sin ( 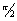- A) cos (- B) + cos ( 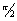- A) sin(- 6)
= cos A cos B - sin A sin B .

3) sin (A + B) = sin A cos B - cos A sin B

4) cos (A + B) = cos A cos B + sin A sin B

5) tan (A + B) =

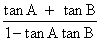
6) tan (A + B) =

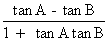
7) cot (A + B) =

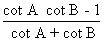
8) cot (A + B) =

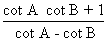
Illustration 3:
If A + B = 45 ⁰, show that (1 + tan A) (1 + tan B) = 2.
Ans:- tan (A + B) =
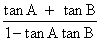
1 = 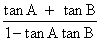( 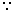A + B = 45^o.so tan (A + B) = 1 )
So, tan A + tan B + tan A tan B = 1
or, tan A + tan B + tan A + tan B + 1 = 2
or, (tan A + 1) (tan B + 1) = 2

Some more farmulae:

1) 2 sin A cos B = sin (A + B) + sin(A - B)
Why ?
Add sin (A + B) = sin A cos B + cosA sin B
& sin (A + B) = sin A cos B - cos A sin B

2) 2cos A sin B =sin(A + B) - sin(A - B)

3) 2cos A cos B =cos(A + B) - cos(A - B)

4) 2sin A sin B =cos(A + B) - cos(A - B)

5) sin C + sin D = 2 sin 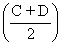cos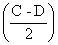
Why ?
Put A + B = C
and A - B = D
in sin (A + B) + sin (A - B) = 2sin A cos B .

6) sin C - sin D = 2 cos 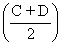sin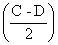

7) cis C + cos D = 2 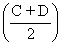cos cos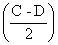

8) cos C - cos D = 2 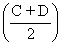sin sin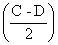

Illustration 4:
Proove that sin 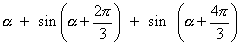= 0
Ans:- sin
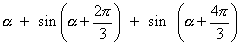
= sin
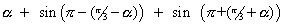
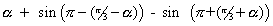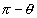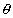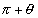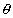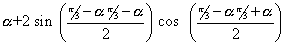
= [ using sin()= sin, sin () = - sin]

= sin
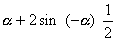
= sin
= sin 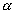- sin - sin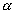
= 0