trignometric-ratios-and-identities-3
Math: Trignometry Chapter
Trignometri Ratios multiples of an angle :
1) sin 2 = 2sin
= 2sin  cos
cos =
= 
why ? sin (A +B) = sin A cos B + cos A sin B
Put A = B =
So, sin 2 = 2sin
= 2sin  cos
cos
=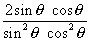
=
2) cos2 = cos2
= cos2 -sin2
-sin2 = 1 - 2 sin2
= 1 - 2 sin2
= cos2 - 1
- 1
=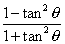
3) tan 2 =
= 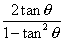
4) sin 3 = 3 sin
= 3 sin  - 4sin2
- 4sin2 
Why ?
sin3 = sin (
= sin ( + 2
+ 2  )
)
sin ( + 2
+ 2 ) = sin
) = sin  cos2
cos2 + cos
+ cos  sin2
sin2
= sin ( 1 - 2 sin2
( 1 - 2 sin2 ) + cos
) + cos (2sin
(2sin cos
cos )
)
= sin - 2sin3
- 2sin3 + 2sin
+ 2sin  (1 - sin2
(1 - sin2 )
)
= 3 sin - 4 sin3
- 4 sin3
5) cos 3 = 4 cos3
= 4 cos3  - 3 cos
- 3 cos
6) tan 3 =
= 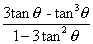
Illustration 5:
sin x + sin y = a and cos x + cos y = b , show that
sin (x + y) =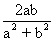 and tan (x - y)
and tan (x - y) 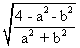
Ans:- sin x + sin y = a
=> 2 sin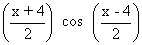 = a ...................(1)
= a ...................(1)
cos x + cos y = b
=> 2 cos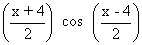 = b ...................(2)
= b ...................(2)
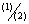 => tan
=> tan 
sin (x + y) =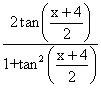
=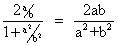
Squaring (1), (2) and adding .
4 cos2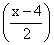
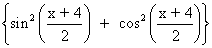 = a2 +b2
= a2 +b2
or cos2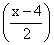 =
= 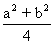
sin2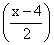 = 1 -
= 1 - 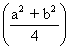
=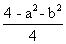
tan2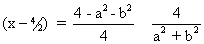
tan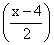 =
= 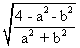
Illustration 6:-
Find the value of sin180 ?
Ans:- Let 180
180
So, 5 = 900
= 900
=> 2 = 900 - 3
= 900 - 3 
Or, sin 2 = sin (900 - 3
= sin (900 - 3 )
)
=> sin 2 =cos3
=cos3
=> 2sin cos
cos = cos
= cos (4 cos2
(4 cos2 - 3)
- 3)
=> 2sin = 4cos2
= 4cos2 - 3 (
- 3 ( 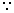 cos
cos
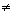 0)
0)
= 1 - 4sin2
=> 4sin2 + 2 sin
+ 2 sin - 1 = 0
- 1 = 0
So, sin =
= 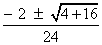
=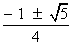
But since sin > 0 we have sin
> 0 we have sin  =
=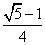
So, sin 18 o =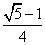
Dumb Question:- Why cos is not equal to 0 ?
is not equal to 0 ?
Ans: cos 900 si O and cos Oo is 1
So, cos being a continous function.
cos i.e. cos 180 would have some value between o and 1.
i.e. cos 180 would have some value between o and 1.
1) sin 2
 = 2sin
= 2sin  cos
cos =
= 
why ? sin (A +B) = sin A cos B + cos A sin B
Put A = B =

So, sin 2
 = 2sin
= 2sin  cos
cos
=
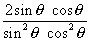
=

2) cos2
 = cos2
= cos2 -sin2
-sin2 = 1 - 2 sin2
= 1 - 2 sin2
= cos2
 - 1
- 1=
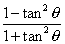
3) tan 2
 =
= 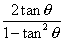
4) sin 3
 = 3 sin
= 3 sin  - 4sin2
- 4sin2 
Why ?
sin3
 = sin (
= sin ( + 2
+ 2  )
)sin (
 + 2
+ 2 ) = sin
) = sin  cos2
cos2 + cos
+ cos  sin2
sin2
= sin
 ( 1 - 2 sin2
( 1 - 2 sin2 ) + cos
) + cos (2sin
(2sin cos
cos )
)= sin
 - 2sin3
- 2sin3 + 2sin
+ 2sin  (1 - sin2
(1 - sin2 )
)= 3 sin
 - 4 sin3
- 4 sin3
5) cos 3
 = 4 cos3
= 4 cos3  - 3 cos
- 3 cos
6) tan 3
 =
= 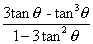
Illustration 5:
sin x + sin y = a and cos x + cos y = b , show that
sin (x + y) =
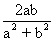 and tan (x - y)
and tan (x - y) 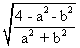
Ans:- sin x + sin y = a
=> 2 sin
 = a ...................(1)
= a ...................(1)cos x + cos y = b
=> 2 cos
 = b ...................(2)
= b ...................(2) => tan
=> tan 
sin (x + y) =
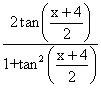
=
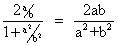
Squaring (1), (2) and adding .
4 cos2
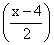
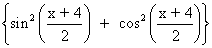 = a2 +b2
= a2 +b2or cos2
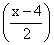 =
= 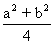
sin2
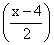 = 1 -
= 1 - 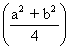
=
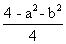
tan2
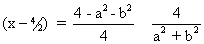
tan
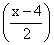 =
= 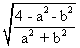
Illustration 6:-
Find the value of sin180 ?
Ans:- Let
 180
180So, 5
 = 900
= 900=> 2
 = 900 - 3
= 900 - 3 
Or, sin 2
 = sin (900 - 3
= sin (900 - 3 )
)=> sin 2
 =cos3
=cos3
=> 2sin
 cos
cos = cos
= cos (4 cos2
(4 cos2 - 3)
- 3)=> 2sin
 = 4cos2
= 4cos2 - 3 (
- 3 (  cos
cos
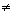 0)
0)= 1 - 4sin2

=> 4sin2
 + 2 sin
+ 2 sin - 1 = 0
- 1 = 0So, sin
 =
= 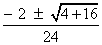
=
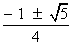
But since sin
 > 0 we have sin
> 0 we have sin  =
=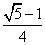
So, sin 18 o =
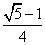
Dumb Question:- Why cos
 is not equal to 0 ?
is not equal to 0 ?Ans: cos 900 si O and cos Oo is 1
So, cos being a continous function.
cos
 i.e. cos 180 would have some value between o and 1.
i.e. cos 180 would have some value between o and 1.