trignometric-ratios-and-identities-4
Some nice manipulations:
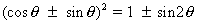
Why ?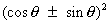 = cos2
= cos2 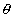 sin2
sin2 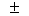 2sin
2sin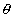 cos
cos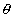
= 1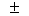 2sin
2sin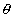 cos
cos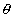
= 1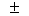 sin2
sin2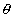
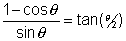
Why ?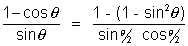
=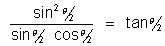
- cos Asin A =
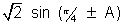
Why !
cos A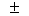 sin A =
sin A = 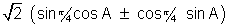
=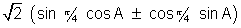
=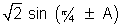
Expressing sin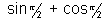 in terms of sin A:
in terms of sin A: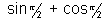 =
= 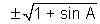
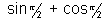 =
= 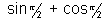
The ambiguity of sign is removed from following figure.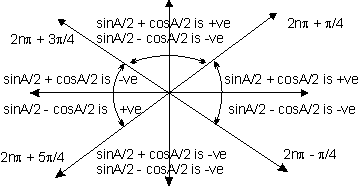
Dumb Question: Where does this diagram come from ?
Ans:-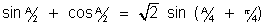
So, if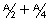 is in I st or IInd quadrent
is in I st or IInd quadrent
then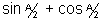 is + ve.
is + ve.
So, A/2 lie from 2n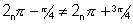 for
for 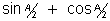 to be + ve
to be + ve
Similarily for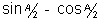
Illustration 7:
If cos 250 + sin 25 0 = P , then find value of cos 500 in trems of P ?
Ans:- cos500 = cos2 25 0 - sin2 250
= (cos 250 + sin250)(cos 250 - sin250)
P(cos250 - sin250)
Also, (cos250 - sin250)2 + (cos250 - sin250)2 = 1 + 1
cos250 - sin250 = +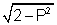
(+ve sign as cos 250 > sin 250)
cos500 =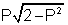
The qreatest and least valume of expression (a sin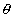 + b cos
+ b cos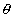 )
)
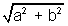
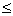 a sin
a sin 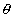 + b cos
+ b cos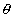
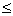
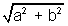
Why?
Let a = r cos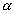
b = r sin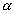 so that r =
so that r = 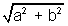
So, a sin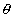 + b cos
+ b cos 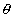 = r (sin
= r (sin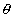 cos
cos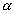 + cos
+ cos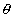 sin
sin 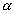 )
)
= r sin (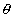 +
+ 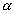 )
)
Now sin (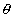 +
+ 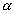 has minimum and maximum value as + 1 and - 1 esppectively.
has minimum and maximum value as + 1 and - 1 esppectively.
So, - r rsin (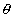 +
+ 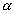 )
)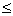 r
r
So, -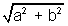
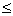 a sin
a sin 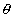 + b cos
+ b cos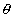
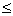
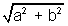
Illustration 8:
Find the minimum and maximum value of
6 sin x cos x + 4cos2 2x ?
Ans:- 6 sin x cos x + 4cos2 2x = (2sin x cos x ) + 4cos 2x
= 3 sin 2x + 4cos 2x .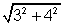 3sin 2x + 4cos2x
3sin 2x + 4cos2x 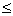
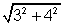
=> Minimum value of 6sin x cos x + 4 cos 2x is - 5
and maximum value is 5.
Sum of sine and cosine senies when angles are in AP .
(1) sin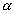 + sin
+ sin 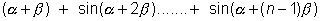 =
= 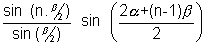
Why ?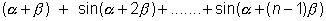
2sin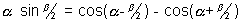
2sin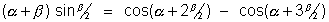
2sin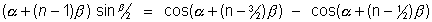
By adding these n lines we have.
2sin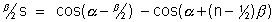
= 2sin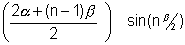
S =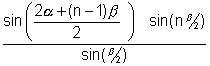
(2)
=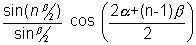
Illustration 9:
Find sum of sin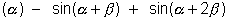 -…………+ 0 n terms. Ans:- Now, sin
-…………+ 0 n terms. Ans:- Now, sin 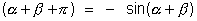
sin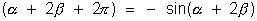
sin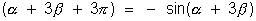
………………………………………………..
Hence the series is
sin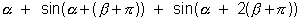 …………
…………
=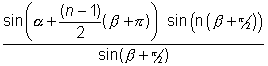
=