trignometric-ratios-and-identities-5
Conditional Identities.
If A + B + C = 180o then .
(i) sin 2A + sin 2B + sin 2c = 4sinA sin B sinC.
Why ?
A + B + C = 180o
So, A + B = 180o - C
sin(A + B) = sin C
cos (A + B) = - cos C
sin 2A + sin 2B + sin 2C = 2 sin (A + B) cos (A - B) + 2sin C cos C.
= 2sin C cos (A - B) + 2sin (- cos (A + B))
= 2sin C (cos (A - B) - cos (A + B))
= 2sin C (2sin A sin B)
= 4sin A sin B sin C .
(ii) cos 2A + cos 2B + cos 2C = - 1 - 4cos A cosB cosC
(iii) sinA + sinB + sinC = 4 cos 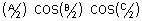
(iv) cosA + cosB + cosC = 1 + 1 + 4sin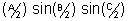
(v) tanA + tanB + tanC =tanA tanB tanC
Why ?
tan (A + B + C) = 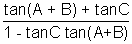
= 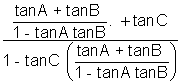
= 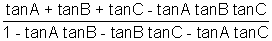
So, since tan (A + B + C) = tan (1800) = 0
So, tanA + tanB + tanC - tanA + tanB + tanC = 0
=> tanA + tanB + tanC = tanA + tanB + tanC.
(vi) cotA + cotB + cotA + cotC + cotB cotC = 1
(vii) 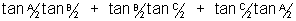
(viii) 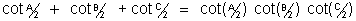
Illustration 10:
If A + B + C = 180 o then prove that
sin2 A + sin2 C = 2 + 2 cosA cosB cosC.
Ans:- sin2A + sin2B + sin2C = 1/2 (1 - cos2A + 1 - cos2B + 1 - cos2C)
= 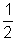 (3 - (cos2A + cos2B + cos2C))
(3 - (cos2A + cos2B + cos2C))
= 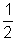 [3 - (- 1 - 4cosA cosB cosC)]
[3 - (- 1 - 4cosA cosB cosC)]
= 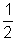 [4 + 4cosA cosB cosC]
[4 + 4cosA cosB cosC]
= 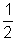 cosA cosB cosC
cosA cosB cosC
= 2 + 2 cosA cosB cosC
- Question - If sin
 + cosec
+ cosec = 2 then what is the value of sin2
= 2 then what is the value of sin2 + coses2
+ coses2 .
.
Solution:- sin2 + cosesc2
+ cosesc2 = (sin
= (sin + cosec
+ cosec )2 - 2sin
)2 - 2sin cosec
cosec
= (1 + 1)2 - 2.1 = 2 - Prove that 2(sin6
 + cos6
+ cos6 ) - 3(sin4
) - 3(sin4 + cos4
+ cos4  ) + 1 = 0
) + 1 = 0
Solution:- L.H.S. 2 [ (sin2 + cos2
+ cos2 )3 - 3sin2cos2
)3 - 3sin2cos2 (sin2
(sin2 + cos2) ] -[ (sin2
+ cos2) ] -[ (sin2 + cos2
+ cos2 )3 - 3sin2cos2
)3 - 3sin2cos2 ] + 1
] + 1
= 2 [ 1 - 3 sin2 cos2
cos2 ] - 3 [ 1 - 2sin2
] - 3 [ 1 - 2sin2 cos2
cos2 ] + 1
] + 1
= 0 - Prove that
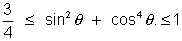 for all real
for all real 
Solution sin2 + cos4
+ cos4 - cos2
- cos2 + 1
+ 1
=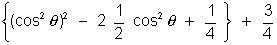
=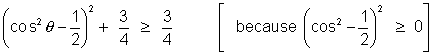
Also, sin2 + cos2
+ cos2 = cos4
= cos4 - cos2 + 1
- cos2 + 1
= cos2 (cos2
(cos2  - 1) + 1
- 1) + 1
= 1 - sin2 cos2
cos2
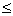 1
1
[ becaise sin2 cos2
cos2
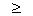 0]
0] - Evaluate sin 78 o - sin66o - sin42 o + sin6o
= (sin 78o - sin42o) - ( sin66o - sin6o)
= 2cos 60o sin18o - 2cos36o. sin30o
= sin18o - cos36o
=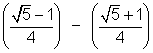
= -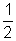
(5) If a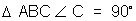 then find the maximum value of sinA sinB .
then find the maximum value of sinA sinB .
Solution:- sinA sinB =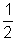
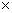 2 sinA sinB
2 sinA sinB
=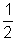 [ cos (A - B) - cos (A + B)]
[ cos (A - B) - cos (A + B)]
=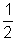 [cos (A - b) - cos 90o]
[cos (A - b) - cos 90o]
=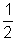 cos (A - B)
cos (A - B) 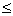
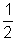
So maximum valuie of sinA sinB =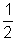
(6) Prove that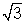 cosec 20o - sec 20o = 4
cosec 20o - sec 20o = 4
Soluction- L.H.S. =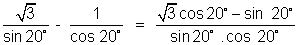
=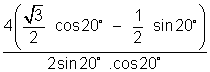
=4.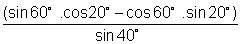
= 4.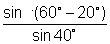
= 4.
= 4 = R.H.S.
(7) Find the value of,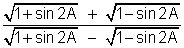
When | tanA | < | and | A | is acure,
Solution:-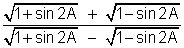
=>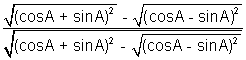
=>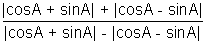
=>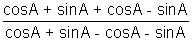
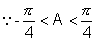 and in this interval casA > sinA }
and in this interval casA > sinA }
=>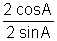 => cotA
=> cotA
When |tanA| < 1 and |A| is acute.
Q. Find a and b such that for all x, a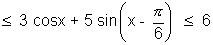
Soluction:- 3 cosx + 5 sin(x -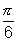 ) = 3 cosx + 5 sinx cos
) = 3 cosx + 5 sinx cos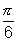 - 5 cosx sin
- 5 cosx sin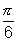
= (3 - 5/2)cosx + 5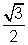 sinx
sinx
=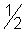 cosx +
cosx + 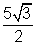 sinx
sinx
a =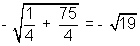
and b =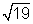
(9) Find the maximum and minimum value of cos2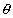 - 6 sin
- 6 sin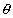 cos
cos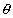 + 3 sin2
+ 3 sin2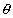 + 2
+ 2
Soluction:- cos2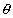 - 6 sin
- 6 sin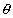 .cos
.cos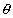 + 3 sin2
+ 3 sin2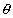 + 2
+ 2
= (1 - sin2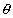 ) - 3 sin2
) - 3 sin2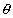 + 3 sin2
+ 3 sin2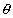 + 2
+ 2
= 2 sin2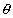 - 3 sin2
- 3 sin2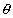 + 3
+ 3
= (1 - cos2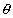 ) - 3sin2
) - 3sin2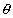 + 3
+ 3
= 4 - (cos2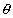 + 3 sin2
+ 3 sin2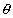 ) …………………………………………. (i)
) …………………………………………. (i)
as we have -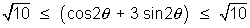
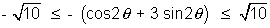
or 4 -