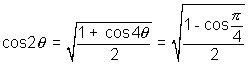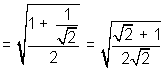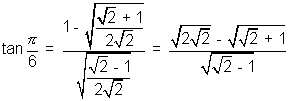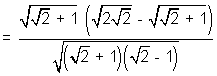trignometric-ratios-and-identities-6

(10) If a triangle ABC show that -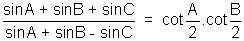
Solution:- Dr = sinA + sinB - sinC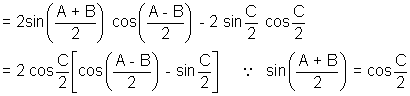


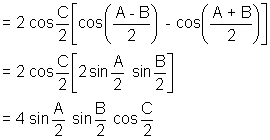
Similarly N_r = 4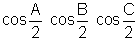
L.H.S. =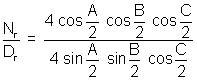
          

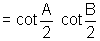
(11) Prove that tanA + 2 tan2A + 4 tan 4A + 8 cot 8A = cot A
L.H.S. = tanA + 2 tan2A + 4 tan4A +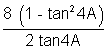
           = tanA + 2 tan2A + 4 cot4A
           = tanA + 2 tan2A + 4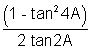
           = tanA + 2 cot2A
           = tanA +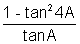
           = cotA = R.H.S.

(12) If 2 cosA = x + 1/x , 2 cosB = y + 1/y show that 2 cos(A - B) = x/y + y/x
Soluction:- 2 cosA = x + 1/x   since   4 sin²A = 4 - 4 cos²A
                             = 4 - (x + 1/x)²
4 sin²A = - [(x + 1/x)² - 4]
4 sin²A = - i²[(x - 1/x)²]
2 sinA = i(x - 1/x)
Similarily 2 cosB = y + 1/y
2 sinB = i(y - 1/y)
Now, 2 cos(A - B) = 2[cosA cosB + sinA sinB]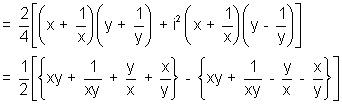

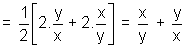= R.H.S.

Medium
Q-1 Determine the smallest positive value of x(in degrees ) for which tan (x + 100⁰) = tan (x + 50⁰) tan x. tan (x - 50⁰)
Soluction:- Rearranging expression-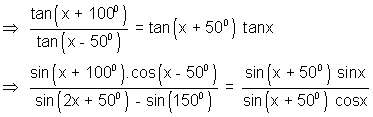


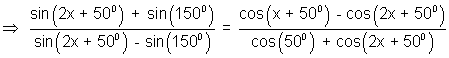
Applying componedo and dividendo, we get-

     
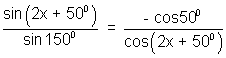
=> cos50^o + 2sin (2x + 50^o) . cos (2x + 50^o) = 0
=> cos 50^o + sin (4x + 100^o ) = 0
=> cos50^o + cos (4x + 10^o ) = 0
=> cos (2x + 30^o) cos(2x - 20^o ) = 0
=> x = 30^o , 55^o
The smallest value of x = 30^o

Dump Question:- Why we rearranged tha (x + 100^o) = tan (x + 50^o)tan x tan(x -50^o)
as 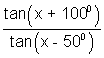= tan(x + 50^o) tanx.
Ans:- Well the motiration behind doing this was the fact that the sum of x + 100^o and x - 50^o is 2x + 50 ^o and also the sum of x + 50^o and x is 2x + 50^o
And, what more the variable x is removed when we substract the one angle from another.
The usefulness of this obserration is clearly when we use compendo and dividerdo.

Question:- If 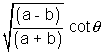, prove that (a - b cos2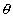)(a - b cos2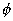) is independent of 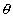and .
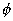Soluction:- Let us put tan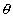 = t₁ and tan 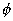= t₂
t₁².t₂² = 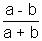………………………………………………… (i)
Also, cot2 =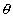
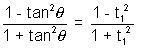
cos2 =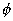
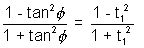
Now a - b cos2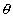 = a - b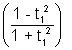
=
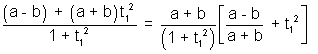
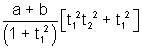=     [by (i)]
=
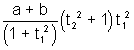
Similarily (a - b cos2) =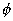
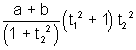
Hence a - b cos2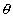)(a - b cos2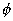) = (a + b)²t₁²t₂² = a² - b²
Which is independent of 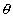and .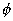

Q. Show that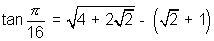
Soluction:- We know 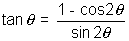where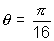
Also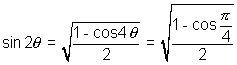
                    
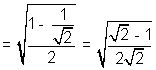
and