trignometric-ratios-and-identities-8
Q-2. Show that 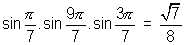
Solution: Let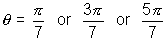 (Note
(Note 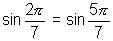 )
)

or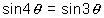
or 2 sin2 cos2
cos2 = 3 sin
= 3 sin - 4 sin3
- 4 sin3
or 4 cos .cos2
.cos2 = 3 - 4 sin2
= 3 - 4 sin2 (
(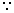 sin
sin
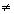 0)
0)
or 4 cos .(2 cos2
.(2 cos2 - 1)
- 1)
This is a third degree equation in cos and each of
and each of 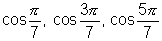 satisfied it.
satisfied it.
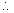 roots of (1) are
roots of (1) are 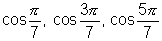
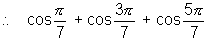 = sum of roots = -
= sum of roots = - 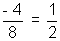 ................................................. (2)
................................................. (2)
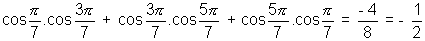 ............................................. (3)
............................................. (3)
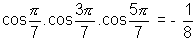 .................................................................................... (4)
.................................................................................... (4)
Now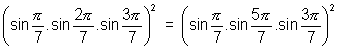
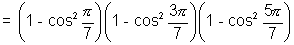
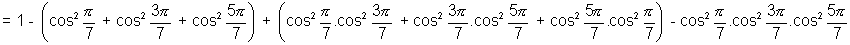
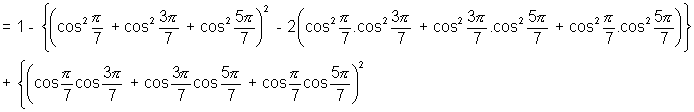
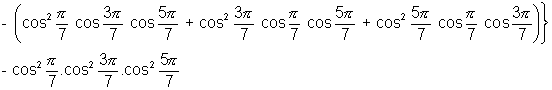
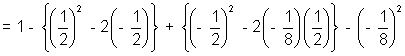 [Using (2), (3), (4)]
[Using (2), (3), (4)]
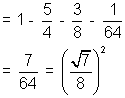
Hence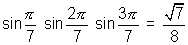
Dumb Question:- How was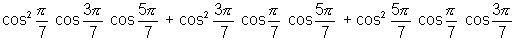 equated to
equated to 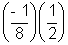 .
.
Ans:-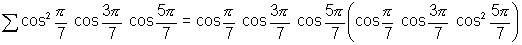
=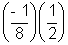
Q-3. If A + B + C =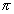 , sinA sinB sinC = P and cosA cosB cosC = 2 then otain the cubic equation whoose roots are tanA, tanB and tanC.
, sinA sinB sinC = P and cosA cosB cosC = 2 then otain the cubic equation whoose roots are tanA, tanB and tanC.
Solution:- The required cubic equation is
(x - tanA)(x - tanB)(x - tanC) = 0
or x3 - (tanA + tanB + tanC) x2 + x(tanA tanB + tanB tanC + tanC tanA) - tanA tanB tanC = 0 ...............................................(1)
Now tanA. tanB. tanC =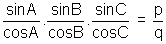 .........................................................................(2)
.........................................................................(2)
Also tan(A + B) = tan(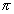 - C) = - tanC
- C) = - tanC
or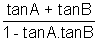 = - tanC
= - tanC
or tanA + tanB + tanC = tanA tanB tanC =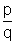 ..............................................................(3) [Using (2)]
..............................................................(3) [Using (2)]
Now sin2A + sin2B + sin2C
=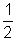 [3 - (cos2A + cos2B + cos2C)]
[3 - (cos2A + cos2B + cos2C)]
=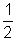 [3 - {2 cos(A + B).cos(A - B) + 2 cos2C - 1}]
[3 - {2 cos(A + B).cos(A - B) + 2 cos2C - 1}]
=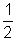 [4 - {- 2cosC cos(A - B) + 2cos2C}]
[4 - {- 2cosC cos(A - B) + 2cos2C}]
=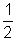 [4 + 2 cosC{cos(A - B) + cos(A + B)}]
[4 + 2 cosC{cos(A - B) + cos(A + B)}]
= 2(1 + cosA cosB cosC) = 2(1 + q)
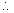 sin2A sin2B sin2C (cosec2B cosec2C + cosec2C cosec2A + cosec2A cosec2B ) = 2(1 + q)
sin2A sin2B sin2C (cosec2B cosec2C + cosec2C cosec2A + cosec2A cosec2B ) = 2(1 + q)
or p2{(1 + cot2B)(1 + cot2C) + (1 + cot2C) (1 + cot2A) + (1 + cot2A) (1 + cot2B)} = 2(1 + q)
or p2{3 + 2 (cot2A + cot2B + cot2C) + cot2B cot2C + cot2C cot2A + cot2A cot2B)} = 2(1 + q)
or p2[3 + 2{cotA + cotB + cotC)2 - 2(cotA cotB + cotB cotC + cotC cotA)} + {(cotB cotC + cotC cotA + cotA cotB)2 - 2 cotA cotB x cotC(cotA + CotB + cotC)}] = 2(1 + q)
or p2 [3 + 2{(cotA + cotB + cotC)2 - 2
+ {1 - 2.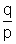 (cotA + cotB + cotC)}] = 2 (1 + q) ..........................................(4)
(cotA + cotB + cotC)}] = 2 (1 + q) ..........................................(4)
[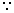 cotA. cotB = 1 if A + B + C =
cotA. cotB = 1 if A + B + C = 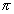 ]
]
Let y = tanA tanB + tanB tanC + tanC tanA
= tanA tanB tanC(cotC + cotA + cotB)
=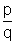 (cotA + cotB + cotC )
(cotA + cotB + cotC )
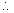 cotA + cotB + cotC =
cotA + cotB + cotC = 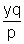 ........................................................(5)
........................................................(5)
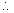 (4) gives
(4) gives
or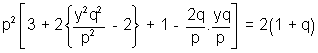
or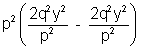 -2(1 + q)
-2(1 + q)
or q2y2 - q2y - (1 - q) = 0
y =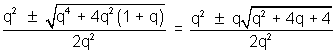
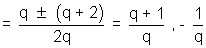 ........................................................... (6)
........................................................... (6)
From (1), (2), (3), (4), (5) and (6),
x3 -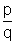 x2 +
x2 + 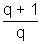 x -
x - 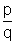 = 0 where y =
= 0 where y = 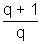
or x3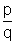 x2 -
x2 - 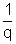 x -
x - 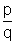
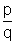 = 0 when y = -
= 0 when y = - 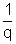
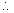 The required equation is
The required equation is
qx3 - px2 + (q + 1)x - p = 0
or qx3 - px2 - x - p = 0
Dumb Question:-
How does suddenly we started evaluating sin2A + sin2B + sin2C ?
Ans:- The aim that we were trying to achievc at that point of time was to calculat the value of tanA tanB + tanB tanC + tan A tanC.
Now when we try to evaluate this we realize that cotA + cotB + cotC needs to evaluated and thus we tried to make a equation is terms of cotA + cotB +cotC
So, all this factors were take in account and then only the sin2A + sin2B + sin2C was eqaluated.
Key words:
(1) Trignometry
(2) Quadrant
(3) Sin
(4) Cos
(5) Tan
(6) Cot
(7) Sec
(8) Cosec
(9) Allied angles.
(10) Compound angles.
(11) Prelendicular
(12) Hypotenuse
(13) Base
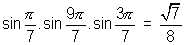
Solution: Let
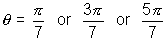 (Note
(Note 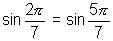 )
)
or
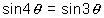
or 2 sin2
 cos2
cos2 = 3 sin
= 3 sin - 4 sin3
- 4 sin3
or 4 cos
 .cos2
.cos2 = 3 - 4 sin2
= 3 - 4 sin2 (
(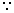 sin
sin
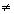 0)
0)or 4 cos
 .(2 cos2
.(2 cos2 - 1)
- 1)This is a third degree equation in cos
 and each of
and each of 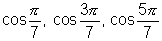 satisfied it.
satisfied it.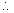 roots of (1) are
roots of (1) are 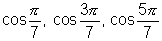
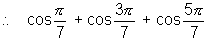 = sum of roots = -
= sum of roots = - 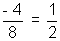 ................................................. (2)
................................................. (2)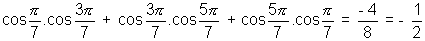 ............................................. (3)
............................................. (3)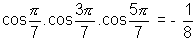 .................................................................................... (4)
.................................................................................... (4)Now
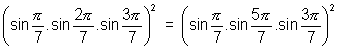
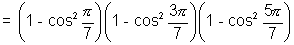
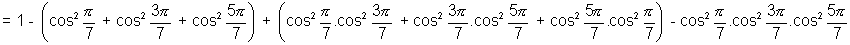
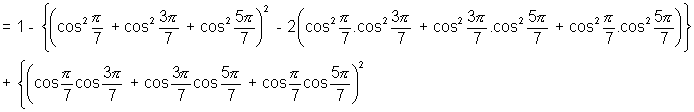
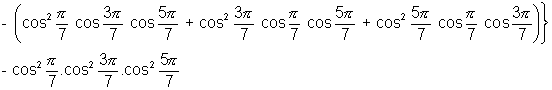
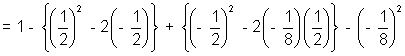 [Using (2), (3), (4)]
[Using (2), (3), (4)]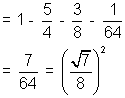
Hence
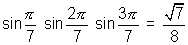
Dumb Question:- How was
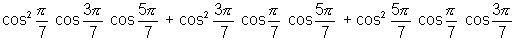 equated to
equated to 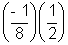 .
.Ans:-
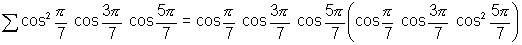
=
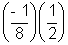
Q-3. If A + B + C =
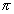 , sinA sinB sinC = P and cosA cosB cosC = 2 then otain the cubic equation whoose roots are tanA, tanB and tanC.
, sinA sinB sinC = P and cosA cosB cosC = 2 then otain the cubic equation whoose roots are tanA, tanB and tanC.Solution:- The required cubic equation is
(x - tanA)(x - tanB)(x - tanC) = 0
or x3 - (tanA + tanB + tanC) x2 + x(tanA tanB + tanB tanC + tanC tanA) - tanA tanB tanC = 0 ...............................................(1)
Now tanA. tanB. tanC =
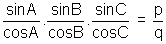 .........................................................................(2)
.........................................................................(2)Also tan(A + B) = tan(
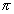 - C) = - tanC
- C) = - tanCor
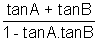 = - tanC
= - tanCor tanA + tanB + tanC = tanA tanB tanC =
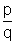 ..............................................................(3) [Using (2)]
..............................................................(3) [Using (2)]Now sin2A + sin2B + sin2C
=
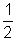 [3 - (cos2A + cos2B + cos2C)]
[3 - (cos2A + cos2B + cos2C)]=
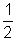 [3 - {2 cos(A + B).cos(A - B) + 2 cos2C - 1}]
[3 - {2 cos(A + B).cos(A - B) + 2 cos2C - 1}]=
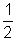 [4 - {- 2cosC cos(A - B) + 2cos2C}]
[4 - {- 2cosC cos(A - B) + 2cos2C}]=
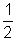 [4 + 2 cosC{cos(A - B) + cos(A + B)}]
[4 + 2 cosC{cos(A - B) + cos(A + B)}]= 2(1 + cosA cosB cosC) = 2(1 + q)
 sin2A sin2B sin2C (cosec2B cosec2C + cosec2C cosec2A + cosec2A cosec2B ) = 2(1 + q)
sin2A sin2B sin2C (cosec2B cosec2C + cosec2C cosec2A + cosec2A cosec2B ) = 2(1 + q)or p2{(1 + cot2B)(1 + cot2C) + (1 + cot2C) (1 + cot2A) + (1 + cot2A) (1 + cot2B)} = 2(1 + q)
or p2{3 + 2 (cot2A + cot2B + cot2C) + cot2B cot2C + cot2C cot2A + cot2A cot2B)} = 2(1 + q)
or p2[3 + 2{cotA + cotB + cotC)2 - 2(cotA cotB + cotB cotC + cotC cotA)} + {(cotB cotC + cotC cotA + cotA cotB)2 - 2 cotA cotB x cotC(cotA + CotB + cotC)}] = 2(1 + q)
or p2 [3 + 2{(cotA + cotB + cotC)2 - 2
+ {1 - 2.
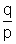 (cotA + cotB + cotC)}] = 2 (1 + q) ..........................................(4)
(cotA + cotB + cotC)}] = 2 (1 + q) ..........................................(4)[
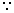 cotA. cotB = 1 if A + B + C =
cotA. cotB = 1 if A + B + C = 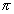 ]
]Let y = tanA tanB + tanB tanC + tanC tanA
= tanA tanB tanC(cotC + cotA + cotB)
=
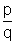 (cotA + cotB + cotC )
(cotA + cotB + cotC )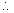 cotA + cotB + cotC =
cotA + cotB + cotC = 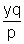 ........................................................(5)
........................................................(5)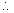 (4) gives
(4) givesor
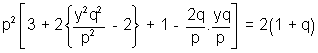
or
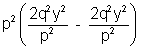 -2(1 + q)
-2(1 + q)or q2y2 - q2y - (1 - q) = 0
y =
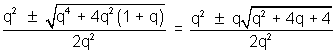
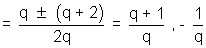 ........................................................... (6)
........................................................... (6)From (1), (2), (3), (4), (5) and (6),
x3 -
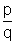 x2 +
x2 + 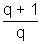 x -
x - 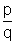 = 0 where y =
= 0 where y = 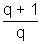
or x3
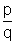 x2 -
x2 - 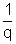 x -
x - 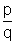
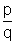 = 0 when y = -
= 0 when y = - 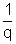
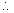 The required equation is
The required equation isqx3 - px2 + (q + 1)x - p = 0
or qx3 - px2 - x - p = 0
Dumb Question:-
How does suddenly we started evaluating sin2A + sin2B + sin2C ?
Ans:- The aim that we were trying to achievc at that point of time was to calculat the value of tanA tanB + tanB tanC + tan A tanC.
Now when we try to evaluate this we realize that cotA + cotB + cotC needs to evaluated and thus we tried to make a equation is terms of cotA + cotB +cotC
So, all this factors were take in account and then only the sin2A + sin2B + sin2C was eqaluated.
Key words:
(1) Trignometry
(2) Quadrant
(3) Sin
(4) Cos
(5) Tan
(6) Cot
(7) Sec
(8) Cosec
(9) Allied angles.
(10) Compound angles.
(11) Prelendicular
(12) Hypotenuse
(13) Base