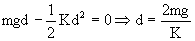The concept of work-energy is universal and is applicable almost in all fields of physics, engineering chemistry, biology etc. However here we analyze the application of work concept in Mechanics. ‘Work’ has much more in it then just a language tool. For example, if a person is holding an object, he gets tired but still does no work. Here we will analyze such myths and also explore the term power. We will also gain an insight into energy approach for solving mechanics problems which were tedious to solve using Newton’s law.
WORK:
When ever force acting on a body is able to actually move it through some distance in the direction of force, the work is said to be done by the force.
The force performing work may be constant or a variable.
Work done by CONSTANT FORCE:
An object undergoes displacement‘s’ along a straight line while acted on by a force F, the angle between 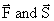 isq. Then work done is
isq. Then work done is
W=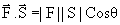
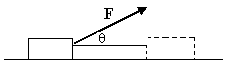
Fig (1)
a) Work done as such has no relevance until the commenced force is maintained.
b) Work is scalar quantity (as indicated by dot product).
c) Unit of work is Joules 1J = 1Kgm2/s2
d) Dimension of work is [ML2T-2]
Other units of Work:

Fig. (2)
Illustration:
1) A block of mass M is pulled along a horizontal surface by applying a force at an angle
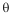
with horizontal. Co-efficient of friction between block and surface is
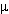
. If the block travels with uniform velocity, find the work done by this applied force during a displacement d of the block.
Solution: The force acting on the block is shown in figure.
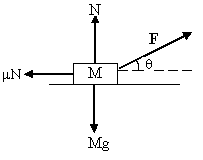
Fig (3)
As the block moves with uniform velocity the force add up to zero.
 FCosq =
FCosq = 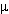 N ---------------- (1)
N ---------------- (1)
FSinq+N= Mg ---------------- (2)
Solving (1) and (2)
FCosq = 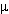 (Mg-FSinq)
(Mg-FSinq)
F = 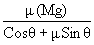
Work done by this force during a displacement d is
W = F.dCosq = 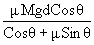
WORK DONE BY VARYING FORCE:
If the force is a variable (i.e. changes) then work done is
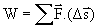 = (Where
= (Where 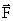 remains constant for displacement Ds)
remains constant for displacement Ds)
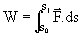 (If
(If 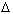 S
S  0 )
0 )
Graphical interpretation of above result:
Work done = Area under F vs. S graph.
Area need to add with sign.
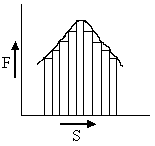
 Fig (4)
Fig (4)
SPRING:
The spring force varies as a lines function of compression or elongation.
F = -KX, where K is stiffness constant of spring.
Work done in on spring:
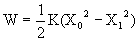
(Initial compression/elongation is X0 and final compression/elongation is X1)
Proof:
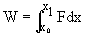 (Assuming force is parallel to displacement)
(Assuming force is parallel to displacement)
= 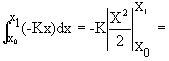
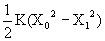
Illustration:
A block of mass m released from rest onto an ideal non-deformed spring of spring constant ‘K’ from a negligible height. Neglecting the air resistance, find the compression ‘d’ of the spring.
Solution:
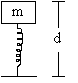
Fig (6)
Here there are two forces involved, weight and spring force.
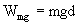 (Work done by weight)
(Work done by weight)
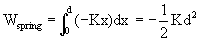
Net work done must be equal to change in kinetic energy (theorem to be discussed in next section).
 K= 0-0 = 0
K= 0-0 = 0
Wmg + Wspring = 0