Work Power Energy -3
WORK ENERGY THEOREM:
Work Energy theorem states that, the net change in Kinetic Energy of a particle (system) is equivalent to the sum of work done by all types of external forces be it conservative or non-conservative.
![]()
Dumb Question:
- Velocity time graph of particle of mass 2kg moving in a straight line is as shown in figure. Find the work done by all the forces on the particle.
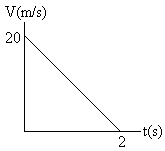
fig.14
Solution:
Initial velocity of particle V0 = 20 m/s,
![]()
![]()
Final velocity of particle vf, ![]()
![]()
From Work energy theorem ![]() = 0-400 = 400.
= 0-400 = 400.
Best thing about work energy theorem is that nature and value of force is not at all required for work equation.
Proof of Work Energy Theorem:
![]() (Multiplying y and dividing by ‘ds’)
(Multiplying y and dividing by ‘ds’)
![]() (Segregating the term)
(Segregating the term)
![]()
Integrating both side
Illustration:
Two bodies A and B connected by a light rigid bar of 10m long and moving in two frictionless guides as shown in the figure. If B starts from rest when it is vertically below A, find the velocity of B when x=6m. Assume mA = mB =200kg and mC = 100kg.
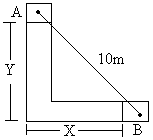
Fig (16)
Solution:
At any instant when the bar is as shown in the figure (16)
![]()
![]() --------- (1)
--------- (1)
![]() ---------- (2)
---------- (2)
Where ![]() velocity of A and
velocity of A and ![]() velocity of B
velocity of B
Including all the three bodies in our system
C move down 6m since B moves 6m along x-axis
Work done by gravity on system = {Work done in moving down A + Work done in moving C}
![]()
Final Kinetic energy of system = Kf = (KA) + (KB) + (KC)
![]()
![]() (Speed of B and C must be same)
(Speed of B and C must be same)
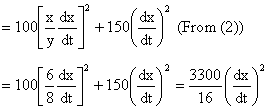
Now from work energy theorem
(Wext)net Here only gravity is external force which is doing work.

Velocity of B at the required moment = 6.9m/s = Ans.
CONSERVATION OF MECHANICAL ENERGY:
Kinetic and Potential energy constitute the mechanical energy of system.
Total Mechanical energy = K+V changes only if
- Energy is converted into other forms like heat, sound etc.
- Work is being done by non-conservative forces like, frictional force
Proof: Let a body undergo displacement Dx under the action of conservative force F. Then from work energy theorem
Kf – Ki = F(x)![]() x --------------- (1)
x --------------- (1)
Since force is conservative hence its potential energy function can also be written as
Vf-Vi= -F(x)![]() x ----------------- (2)
x ----------------- (2)
Adding (1) and (2)
(Vf+Kf)- (Ki+Vi) = F(x) Dx - F(x) Dx
= 0
Vf+Kf = Ki+Vi
Initial Mechanical energy = Final Mechanical energy.
Important Points regarding Conservation Principle:
- If friction and drag are present then mechanical energy will not be conserved
- Conservation of mechanical energy applies only to isolated systems.
- Initial and final states of system must be clearly identified before applying conservation principle.
Illustration:
A block of mass m is pushed against a spring of spring constant K fixed at one end to a wall. The block can slide on a frictionless table as shown in figure. The natural length of the spring is L0 and it is compressed to half its natural length when the block is released. Find the velocity of the block as a function of its distance x from the wall.
Solution:
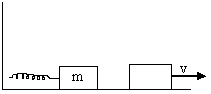
Fig (18)
When the Block is released the spring pushes it towards right. The velocity of the block increases till the spring acquires its natural length. There after the block loses contact with the spring and moves with constant velocity. Initially the compression in the spring
=
When the distance of block from the wall becomes its where x< the compression is (L0-x)
Using the principle of conservation of energy
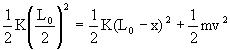
Solving this
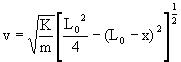
When the spring acquires its natural length x = L0
We have then
There after the block continues with this velocity.