Work Power Energy -5

Derivation:

Motion in a vertical circle:
A particle of mass m is attached to inextensible light string of length l and it is imparted a velocity u in horizontal direction lowest point. Let v be its velocity at point B of circle.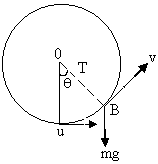

          Fig (23)
Here h = R (1-Cosq)                                                               ------------ (1)
By conservation of mechanical energy

Necessary centripetal force is provided by the resultant of tension T and mgCos

Now three condition arise depending on u,

The string does not stuck at highest point if T 0 at =,
So substituting T = 0 and = for completing the circle in (B)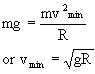
                                    (At highest point)
And h = 2R
So from equation (2)

Or
Or
the particle will complete the circle.
Substituting q = 00 and v = u = in equation (3) we get T = 6mg. So in the critical condition tension in the string at lowest position is 6mg.

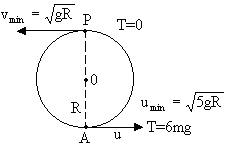
Fig (24)

Putting T = 0 before reaching highest point for

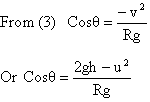
Substituting in equation (1) we get

Velocity of particle becomes zero when
0 = u2-2gh

Now the particle will leave the circle if tension in the string becomes zero but velocity is not zero or,
T = 0 but v 0 this is possible only when
h1<h2

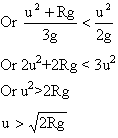
Therefore if

the particle leaves the circle.

The particle will oscillate if velocity of the particle becomes zero but tension in the string is not zero.
V = 0 but T

0 this is possible only when
h2 < h1

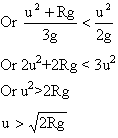
Further if h1 = h2,

and tension and velocity both becomes zero simultaneously.

Illustration:
A ball of mass m slides without friction down a path from height h and then moves in loop of radius Find the force exerted on the ball by the track at B and at C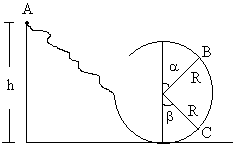

Fig (27)
Solution: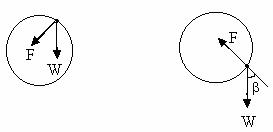

Fig (28)
For maintaining circular motion net centripetal force must be greater than
On applying energy conservation between point A and C we get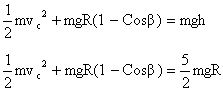

On solving
From f.b.d of body
On solving F_B=3mg (1+Cosb)
Similarly for point B
mg [h-(R+RCosa)] = (energy equilibrium)

F_B = 3mg (1-Cosa)

Related Guides