Work Power Energy -7
PROBLEMS (EASY)
- Force acting on a particle varies with x as shown in figure (33) .Calculate the work done by the force as the particle moves from x = 0 to x = 6m.
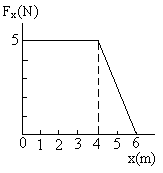
Fig (33)
Solution: The work done by the force is equal to the area under the curve from x=0 to x=6.0m. This area is equal to the area of the rectangular section from x = 0m to x = 4.0m plus the area of the triangular section from x = 4.0m to x = 6m.
2) The mass system is kept on sphere. Ball 1 is slightly disturbed. What is the velocity of these balls when it is making angle ‘q’ with horizontal (friction is absent everywhere).
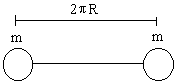
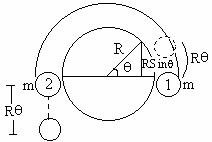
Fig (34)
Solution:
Since they are connected by inextensible string, therefore at any stage the velocity of both particle will be same. Let it be ‘V’.![]() From work energy theorem:
From work energy theorem:![]() (Only external force is gravity)
(Only external force is gravity)![]()
![]()
3) What is the minimum value of ‘u’ for completing circular motion of particle as shown in figure (35)?
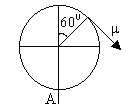
Fig (35)
Solution:
Choosing zero of potential energy at level of A.
If V1 is the velocity at ‘A’ then from energy conservation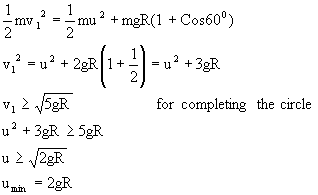
4) A block is projected horizontally on rough horizontal floor. The coefficient of friction between the block and the floor is m. The block strikes a light spring of stiffness K with velocity v0. Find the maximum compression of the spring.
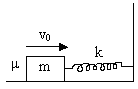
Fig (36)
Solution:
Since the block slides and the spring is compressed through a distance ‘x’ the net retarding force acting on it.
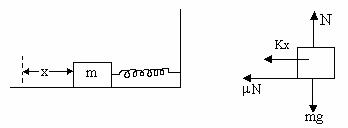
Fig (37)
= F = - (kx +mN) = - (mmg+kx)
Þ Work done by net force for the displacement x,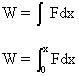
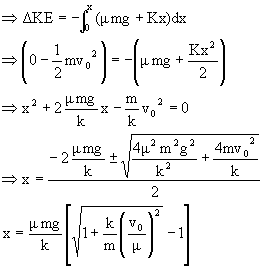
5) In figure 38-A and 38-B AC, DE and EF are fixed inclined planes BC = EF and AB = DE = y. A small block of mass m is released from rest from the point A. It slides down AC and reaches C with a speed VC. The same block is released from rest from the point D, it slides down DEF and reaches the point F with speed VF. The coefficient of kinetic friction between the block and the surface AC and DEF is a, calculate VC and VF.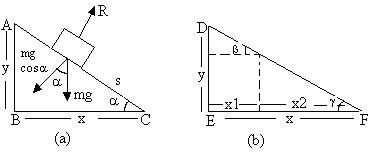
Fig (38)
Solution:
a) ME at A = mgY+0 and if VC is the velocity at C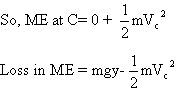
This Loss in ME is equal to work done against friction i.e.![]()
![]() (As Cosa = x/s)
(As Cosa = x/s)![]()
b) In this situation,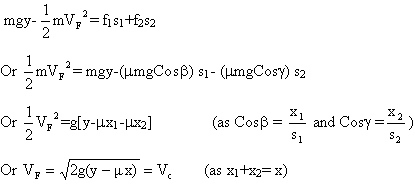
6) A locomotive of mass m starts moving so that its velocity v is according to the law![]() where a is constant and s is distance covered. Find the total work done by all the forces acting the locomotive during the first t seconds after the beginning of motion.
where a is constant and s is distance covered. Find the total work done by all the forces acting the locomotive during the first t seconds after the beginning of motion.
Solution:
Given, differentiating ![]() w.r.t ‘t’ we get
w.r.t ‘t’ we get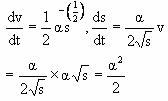
Accelerating ![]() now force acting on locomotive
now force acting on locomotive![]()
Here u =0
Now using ![]() we have
we have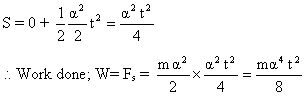
7) The Kinetic energy of a particle moving along a circle of radius R depends on the distance covered S and T = as2, where a is constant. Find the force acting on the particle as a function of S.
Solution:
Differentiating both sides w.r.t ‘t’ we have![]()
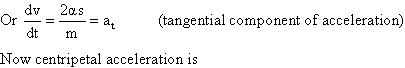

a = 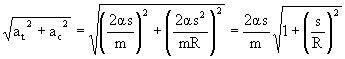
Now force acting on the particle is given by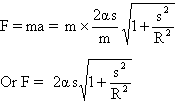
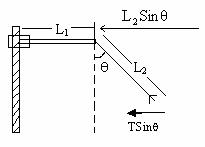
Fig (39)
- = angular speed T = Tension in the string.
Ball moves in horizontal circle with radius r = L1+L2Sinq along vertical direction,
TCosq = mg ----------- (1)
Along radial direction, TSinq = mrw2 ----------- (2)
Using (1) and (2)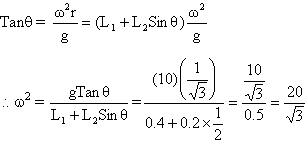
w = 3.398 rad/s
9) A smooth, light rod AB can rotate about a vertical axis passing through its end A. The rod is fitted with small sleeve of mass m attached to the end A by a weightless spring of length l0, stiffness k. What work must be performed to slowly get this system going and the angular velocity w?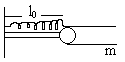
Fig (40)
Solution:
The mass m rotates in a circle of radius l, which is extended length of the spring.
Centripetal force on m = k (l- l0) = mw2l![]()
\W = change in KE of m+ energy stored in the spring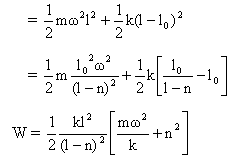
10) A spring gun having spring constant 100 N/m, a small ball of mass 0.1Kg is placed in its barrel by compressing the spring through 0.05m as shown in figure (41)
a) Find the velocity of the ball when spring is released
b) Where should a box is placed on ground so that ball falls in it, if the ball leaves the gun horizontally at a height of 2m above the ground.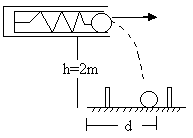
Fig (41)
Solution:
- When the spring is released its elastic potential energy is converted into kinetic energy.
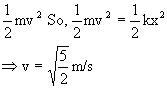
- As vertical component of velocity of ball is zero.
Time taken by the ball to reach the ground,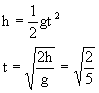
So, the horizontal distance traveled by the ball in this time![]()