Work Power Energy -8
PROBLEMS (MODERATE)
1) A hemispherical bowl of radius R = 0.1m is rotating about its own axis (which is vertical), with an angular velocity w. A particle of mass 10-2Kg on the frictionless inner surface of the bowl is also rotating with the same w. The particle is at a height h from the bottom of the bowl.
a) Obtain the relation between h and w. What is the minimum value of w needed, in order to have a non-zero value of h?
b) It is designed to measure g (acceleration due to gravity) using this step-up, by measuring h accurately. Assuming that R and w are known precisely and that the least count in the measurement of h is 10-4m, what is its minimum possible error Dg in the measured value of g?
Solution:
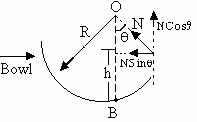
Fig (42)
a) Along x-direction, NSinq = m (AC) w2
Þ NSinq = m (RSinq) w2
N = mRw2 --------------- (1)
Along y-direction, NCosq = mg -------------- (2)
Using (1) and (2)
mRw2Cosq = mg
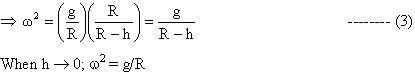
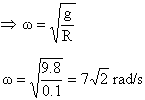
b) From (3), g = (R-h) 2
\Dg = -Dh w2
|Dg|min = |Dh| w2min = ![]()
2) A small body is placed on the top of a smooth hemisphere of radius R. When the sphere is given a uniform horizontal acceleration a0 the body starts sliding down. a) Find the velocity of body relative to sphere at the instant of loosing contact b) Find the angle Æ between radius vector drawn to the body from center of sphere at the time of loosing contact if a0 = g
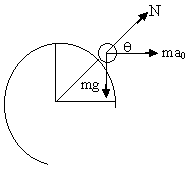
Fig (43)
a) Drawing f.b.d in frame of reference of particle.
![]()
From work energy theorem
![]()
![]()
For just loosing contact N = 0 then using (1) and (2)
Eliminating a0 from (1) and (2) gives
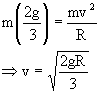
b) Equating (1) and (2) gives
2g (1-Sinq) + 2a0Cosq = gSinq - a0Cosq
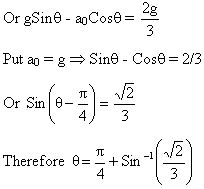
3) A small bar A resting on a smooth horizontal plane is attached by threads to a point P as shown in figure. And by P means of a weightless pulley to weight B possessing the same mass as the bar itself. Beside, the bar is also attached to a point O by means of a light non deformed spring of length l0 = 50cm and with spring constant K, then find the velocity?
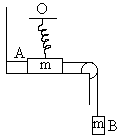
Fig (44)
Solution:
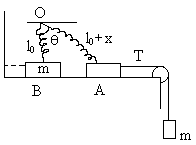
Fig (45)
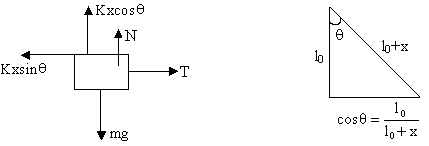
Drawing the f.b.d of A for just breaking off
N = KxCosq = mg =0
Þ KxCosq = mg

From (1) and (2)
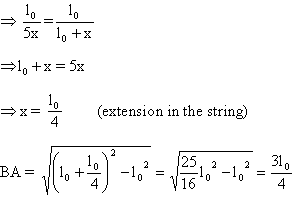
Mass B would have moved same distance downwards
Since they are connected with inextensible string hence velocity of A and B would be same.
Now from energy conservation,
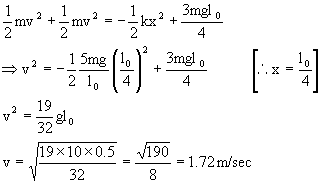
4) A horizontal plane support a stationary vertical cylinder of radius R and disc A attached to the cylinder by a horizontal thread AB of length l0. An initial velocity v0 is imported to the disc as shown. How long will it move along plane until it strikes against the cylinder? The friction is assumed to be absent.
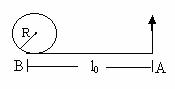
Fig (46)
Solution:
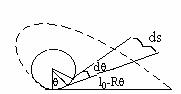
Fig (47)
ds = (l0-R
If
the path traversed by disc
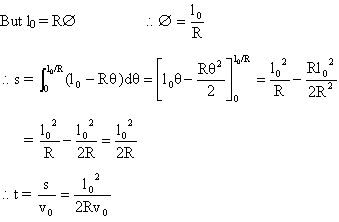
Dumb Question:
- How is l0 = R
 ?
?
Ans: Suppose the final picture is fig.(48). The whole thread rolls over the cylinder, then as obvious the length l0 = R![]() .
.
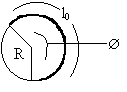
Fig (48)
- How the motion does become a projectile motion?
Ans: Note that at point B, the string becomes slack, so there is no tension acting over the particle. Now the particle has some velocity and gravity is acting over it, so it starts projectile motion at B and ends at A.